ベイス統計における単回帰分析

頻度主義とベイズ統計のそれぞれの単回帰分析を行いました。

• これからベイス統計をやってみたい人
• StanとRを使って何か始めたい人
  向けです。

参考にした本

• StanとRでベイズ統計モデリング
• パターン認識と機械学習（上）

頻度主義による単回帰分析

頻度主義とは、一般的に単回帰分析と言う場合の手法である。真の母数（パラメータ）があって、それを得られた実データを通して推定するやり方である。真のパラメータを推定する方法として、最尤推定、つまり尤度が最大になるようなパラメータを求める。
ノイズとして正規分布を仮定すると、最尤推定による方法は、最小二乗法と一致する。

> data <- mtcars
> head(data)
                   mpg cyl disp  hp drat    wt  qsec vs am gear carb
Mazda RX4         21.0   6  160 110 3.90 2.620 16.46  0  1    4    4
Mazda RX4 Wag     21.0   6  160 110 3.90 2.875 17.02  0  1    4    4
Datsun 710        22.8   4  108  93 3.85 2.320 18.61  1  1    4    1
Hornet 4 Drive    21.4   6  258 110 3.08 3.215 19.44  1  0    3    1
Hornet Sportabout 18.7   8  360 175 3.15 3.440 17.02  0  0    3    2
Valiant           18.1   6  225 105 2.76 3.460 20.22  1  0    3    1

まずは散布図を書く。mpgでdispは負の相関がありそうで、これを単回帰分析してみる。

> library(ggplot2)
> library(GGally)
> ggpairs(data[c(1:3)])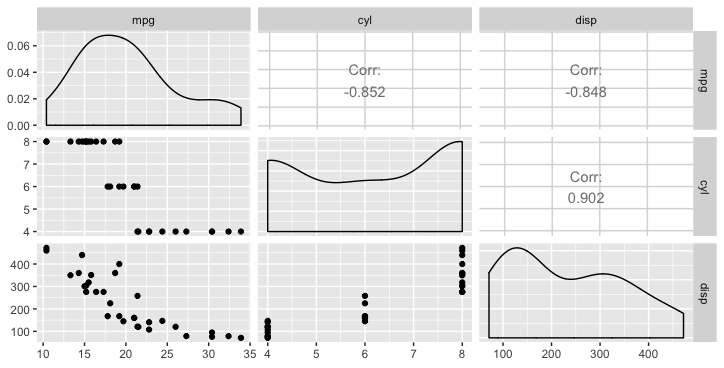

回帰分析はRで非常に簡単に行うことができる。頻度主義による単回帰分析では、切片と傾きが推定するパラメータとなる。下の結果から、mpgに対する傾きは-17.429で、P値も非常に小さい。

> res_lm <- lm(disp ~ mpg, data)
> summary(res_lm)

Call:
lm(formula = disp ~ mpg, data = data)

Residuals:
    Min      1Q  Median      3Q     Max 
-103.05  -45.74   -8.17   46.65  153.75 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  580.884     41.740  13.917 1.26e-14 ***
mpg          -17.429      1.993  -8.747 9.38e-10 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 66.86 on 30 degrees of freedom
Multiple R-squared:  0.7183,    Adjusted R-squared:  0.709 
F-statistic: 76.51 on 1 and 30 DF,  p-value: 9.38e-10

予測区間をプロットすると以下のようになる。下には信頼区間のデータフレームも作成。

> mpg_new <- data.frame(mpg=5:40)
> conf_95 <- predict(res_lm, mpg_new, interval='confidence', level=0.95)
> conf_95 <- data.frame(mpg_new, conf_95)
> pred_95 <- predict(res_lm, mpg_new, interval='prediction', level=0.95)
> pred_95 <- data.frame(mpg_new, pred_95)
> conf_50 <- predict(res_lm, mpg_new, interval='confidence', level=0.50)
> conf_50 <- data.frame(mpg_new, conf_50)
> pred_50 <- predict(res_lm, mpg_new, interval='prediction', level=0.50)
> pred_50 <- data.frame(mpg_new, pred_50)
> p <- ggplot() + 
+      geom_ribbon(data=pred_95, aes(x=mpg, ymin=lwr, ymax=upr), alpha=1/6) +
+      geom_ribbon(data=pred_50, aes(x=mpg, ymin=lwr, ymax=upr), alpha=2/6) + 
+      geom_point(data=data, aes(x=mpg, y=disp), shape=1, size=5) + 
+      geom_line(data=pred_50, aes(x = mpg, y=fit), size=1)
> p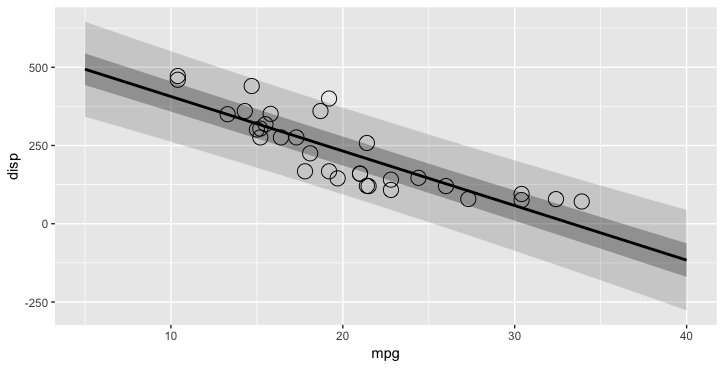

ベイズ統計による単回帰分析

パラメータを確率変数として、その確率分布を求める方法である。データが与えられた時のパラメータ（この場合切片と傾きとノイズ項である正規分布の標準偏差）の確率分布である事後分布を求める。事後分布は尤度関数と事前分布の積に比例する。事後分布を解析的に求める代わりに、尤度関数と事前分布の積からの乱数サンプルを発生させて、事後分布の確率分布を求める。（マルコフ連鎖モンテカルロ法：MCMC）
StanとそのRのパッケージrstanを用いることでこれを簡単に実現できる。

> library(rstan)
> library(ggplot2)
> d <- mtcars
> X_new <- 5:40
> data <- list(N=nrow(d), X=d$mpg, Y=d$disp, N_new=length(X_new), X_new=X_new)

ここでdataはデータをrstanモデルに渡すためのインターフェースになる。実データXとYを渡すのはモデル作成に必要なのは当然として、新たなX_newに対する予測値もstan側で計算できる。
次にstanモデルファイルを作成、下記のようになる。事前確率は、無情報事前分布として指定しない。

data {
    int N;
    real X[N];
    real Y[N];
    int N_new;
    real X_new[N_new];
}

parameters {
    real a;
    real b;
    real<lower=0> sigma;
}

transformed parameters {
    real y_base[N];
    for (n in 1:N)
        y_base[n] = a + b * X[n];
}

model {
    for (n in 1:N)
        Y[n] ~ normal(a + b*X[n], sigma);
}

generated quantities {
    real y_base_new[N_new];
    real y_new[N_new];
    for (n in 1:N_new) {
        y_base_new[n] = a + b * X_new[n];
        y_new[n] = normal_rng(y_base_new[n], sigma);
    }
}

次に実行していく。

> stanmodel <- stan_model(file='model/stan_model_gen.stan')
> fit <- sampling(
+    stanmodel,
+    data=data,
+    init=function() {
+        list(a=runif(1,-10,10), b=runif(1,0,10), sigma=10)
+    },
+    seed=1234,
+    chains = 4, iter = 1000, warmup=200, thin=2
+ )

summary(fit)で各パラメータの平均・標準偏差・quantileが確認できる。

> summary(fit)$summary[1:3,]
           mean    se_mean        sd      2.5%       25%       50%       75%     97.5%
a     580.64605 1.64718267 44.941920 489.55591 550.84505 580.97156 608.79399 674.98920
b     -17.40673 0.07826705  2.129865 -21.50982 -18.77598 -17.40987 -15.99211 -13.25749
sigma  70.21658 0.28515275  9.796146  54.33300  63.44965  69.08561  75.85365  92.45533
          n_eff      Rhat
a      744.4229 1.0020684
b      740.5362 1.0011071
sigma 1180.1994 0.9996721

傾きbの平均値は-17.40673で、頻度主義における単回帰分析の結果と非常に近いことがわかる。ベイズ的なやり方のメリットとして、傾きbの確率分布（平均と標準偏差など）を把握でき理解しやすい。

ms <- rstan::extract(fit)

data.frame.quantile.mcmc <- function(x, y_mcmc, probs=c(2.5, 25, 50, 75, 97.5)/100) {
    qua <- apply(y_mcmc, 2, quantile, probs=probs)
    d <- data.frame(X=x, t(qua))
    colnames(d) <- c('X', paste0('p', probs*100))
    return(d)
}

ggplot.5quantile <- function(data) {
    p <- ggplot(data=data)
    p <- p + theme_bw(base_size=18)
    p <- p + geom_ribbon(aes(x=X, ymin=p2.5, ymax=p97.5), fill='black', alpha=1/6)
    p <- p + geom_ribbon(aes(x=X, ymin=p25, ymax=p75), fill='black', alpha=2/6)
    p <- p + geom_line(aes(x=X, y=p50), size=1)
    return(p)
}

> d_est <- data.frame.quantile.mcmc(x=X_new, y_mcmc=ms$y_new)
> p <- ggplot.5quantile(data=d_est)
> p <- p + geom_point(data=d, aes(x=mpg, y=disp), shape=1, size=5)
> p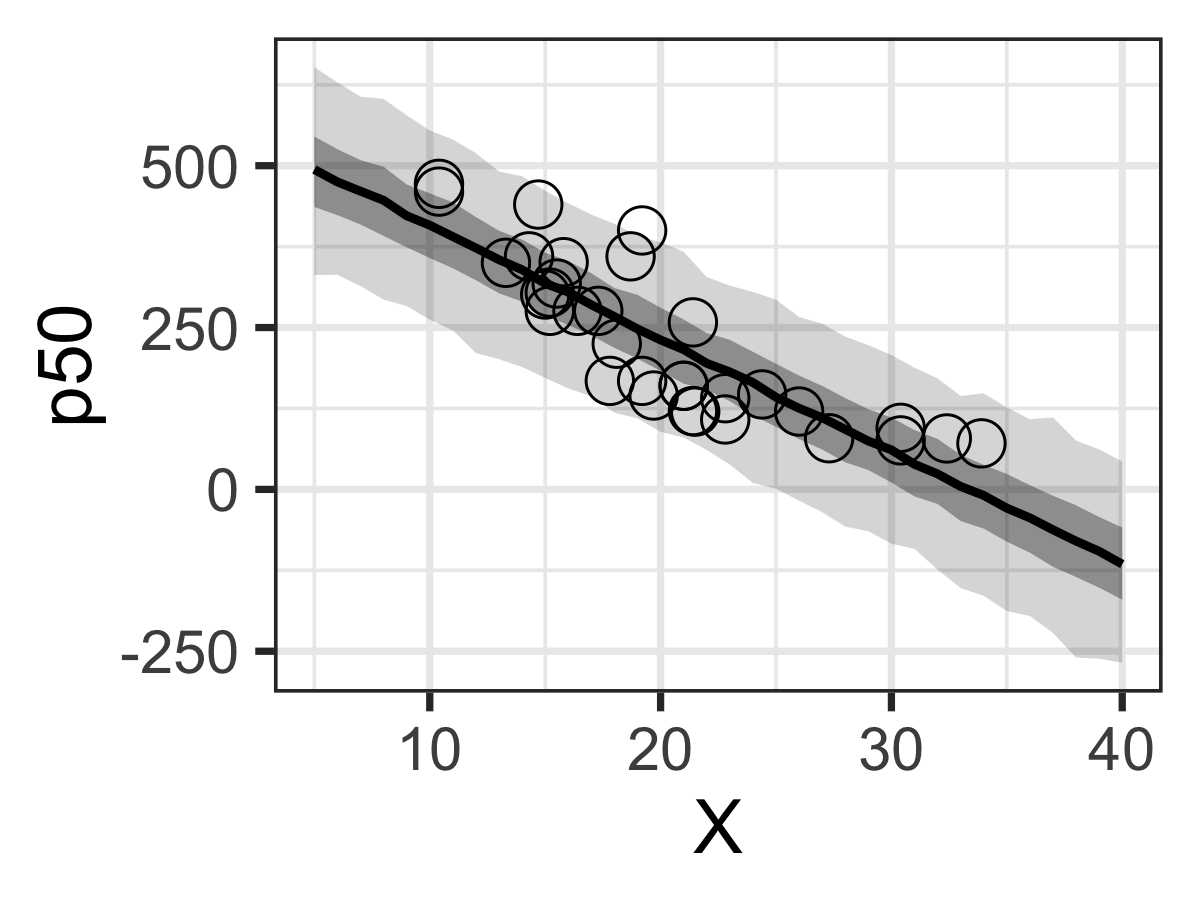

役に立った方はtwitterなどでフォローください。